Aritmética Binaria

1. SUMA DE NÚMEROS BINARIOS

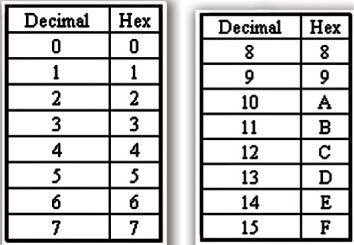
Para sumar número binarios es necesario convertir el dígito binario a decimal (simplemente el 1 transformarlo en 2), sumar en binario y volver a transformarlo a número decimal. Así, se cumple que...
          -1bin + 0bin = 1dec = 1 bin
          -1bin + 1bin = 1dec + 1dec = 2dec = 10 bin
          -1bin + 1bin + 1bin = 1dec + 1dec + 1dec = 3dec = 11 bin (así sucesivamente)

En los casos donde el resultado tiene dos dígitos, el primero pasa a sumarse a la cifra siguiente. Para entenderlo mejor, un ejemplo de suma de números binarios es el siguiente:





2. RESTA DE NÚMEROS BINARIOS

Para restar números binarios, hay que seguir los siguientes pasos:

         1) Completar el sustraendo con ceros.

         2) Cambiar los unos por ceros del sustraendo (este paso se denomina 'calcular el complemento a uno')

         3) Sumo 1 (en binario) al sustraendo (este paso se denomina 'calcular el complemento a dos')

         4) Sumar en binario.

         5) IMPORTANTE: Nunca el resultado puede tener más dígitos que el minuendo o sustraendo.


         

Conversiones

1. CONVERTIR DE DECIMAL A BINARIO

Hay que dividir sucesivamente entre 2 (el número binario) y coger los restos de empezando por abajo.

Importante: Dividir hasta que el cociente de la última división sea 0.





2. CONVERTIR DE BINARIO A DECIMAL

Cada dígito de un número binario se asocia a una potencia de base 2, siendo el primer dígito (empezando por la derecha) 2 elevado a 0, el siguiente 2 elevado a 1, ... y así sucesivamente. Posteriormente, solo se toman los valores de los dígitos 1, y el resultado de sumarlos es el número binario.

Así, el proceso sería el siguiente:





3. CONVERTIR DE DECIMAL A HEXADECIMAL

Hay que dividir sucesivamente entre 16 (en número decimal) y coger los restos empezando por abajo. 

Importante: Dividir hasta que el cociente de la última división sea 0.

Además, como el sistema hexadecimal utiliza 16 dígitos, a partir del dígito 9 (del 10 al 15) a cada dígito se le asocia una letra del abecedario, siendo:



Por tanto, el proceso sería el siguiente:

 RESULTADO: 74D



4. CONVERTIR DE BINARIO A HEXADECIMAL

Primero, se cogen paquetes de 4 bits empezando por la derecha.

Después, dichos paquetes binarios se pasan a decimal

Por último, los números decimales resultantes del paso anterior se convierten a hexadecimal (utilizando la tabla de decimal a hexadecimal del punto 3)


(Donde 3dec es 3hex, A es 10hex y 6dec es 6hex)



5. CONVERTIR DE HEXADECIMAL A DECIMAL

Para hacer esta conversión, es necesario hacer un paso intermedio, en el cual cada dígito del número hexadecimal se convierte a decimal (utilizando la tabla del sistema decimal del punto 3).

Después, teniendo en cuenta el paquete de cuatro bits 8 4 2 1 (que serían las potencias de base dos resueltas), coger aquellos valores que al sumarlos den el número decimal. Estos valores se representarán como 1 (si se cogen) y 0 (si no han sido sumados).

Posteriormente, los paquetes de cuatro bits hay que unirlos, dando como resultado el número binario final.

(Donde 9hex es 9dec, F es 15dec y 2hex es 2dec)

Código ASCII

El código ASCII

El código ASCII (American Standard Code for Information Interchange) es un código de caracteres basado en el alfabeto latino.

El código ASCII básico (no extendido), utilizando 7 bits, es capaz de representar 128 caracteres (enumerados del 0 al 127).

La siguiente tabla muestra el código ASCII extendido: