Hay que dividir sucesivamente entre 2 (el número binario) y coger los restos de empezando por abajo.
Importante: Dividir hasta que el cociente de la última división sea 0.

2. CONVERTIR DE BINARIO A DECIMAL
Cada dígito de un número binario se asocia a una potencia de base 2, siendo el primer dígito (empezando por la derecha) 2 elevado a 0, el siguiente 2 elevado a 1, ... y así sucesivamente. Posteriormente, solo se toman los valores de los dígitos 1, y el resultado de sumarlos es el número binario.
Así, el proceso sería el siguiente:

3. CONVERTIR DE DECIMAL A HEXADECIMAL
Hay que dividir sucesivamente entre 16 (en número decimal) y coger los restos empezando por abajo.
Importante: Dividir hasta que el cociente de la última división sea 0.
Además, como el sistema hexadecimal utiliza 16 dígitos, a partir del dígito 9 (del 10 al 15) a cada dígito se le asocia una letra del abecedario, siendo:
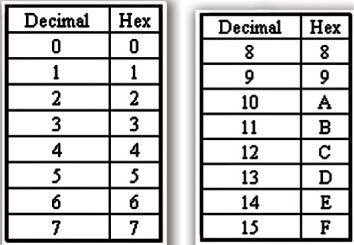
Por tanto, el proceso sería el siguiente:
 RESULTADO: 74D
RESULTADO: 74D4. CONVERTIR DE BINARIO A HEXADECIMAL
Primero, se cogen paquetes de 4 bits empezando por la derecha.
Después, dichos paquetes binarios se pasan a decimal
Por último, los números decimales resultantes del paso anterior se convierten a hexadecimal (utilizando la tabla de decimal a hexadecimal del punto 3)

(Donde 3dec es 3hex, A es 10hex y 6dec es 6hex)
5. CONVERTIR DE HEXADECIMAL A DECIMAL
Para hacer esta conversión, es necesario hacer un paso intermedio, en el cual cada dígito del número hexadecimal se convierte a decimal (utilizando la tabla del sistema decimal del punto 3).
Después, teniendo en cuenta el paquete de cuatro bits 8 4 2 1 (que serían las potencias de base dos resueltas), coger aquellos valores que al sumarlos den el número decimal. Estos valores se representarán como 1 (si se cogen) y 0 (si no han sido sumados).
Posteriormente, los paquetes de cuatro bits hay que unirlos, dando como resultado el número binario final.

(Donde 9hex es 9dec, F es 15dec y 2hex es 2dec)
No hay comentarios:
Publicar un comentario